Tau (mathematics)

An arc of a circle with the same length as the radius of that circle corresponds to an angle of 1 radian. A full circle corresponds to a full turn, or approximately 6.28 radians, which is expressed here using the Greek letter tau (τ).

A comparison of angles expressed in degrees and radians.

This article is about the proposed mathematical constant. For other uses, see Tau § Mathematics.

The number 𝜏 (/ˈtaʊ, ˈtɔː, ˈtɒ/ ^ⓘ; spelled out as tau) is a mathematical constant that is the ratio of a circle's circumference to its radius. It is approximately equal to 6.28 and exactly equal to 2π.

𝜏 and π are both circle constants relating the circumference of a circle to its linear dimension: the radius in the case of 𝜏; the diameter in the case of π.

While π is used almost exclusively in mainstream mathematical education and practice, it has been proposed, most notably by Michael Hartl in 2010, that 𝜏 should be used instead. Hartl and other proponents argue that 𝜏 is the more natural circle constant and its use leads to conceptually simpler and more intuitive mathematical notation.

Critics have responded that the benefits of using 𝜏 over π are trivial and that given the ubiquity and historical significance of π a change is unlikely to occur.

The proposal did not initially gain widespread acceptance in the mathematical community, but awareness of 𝜏 has become more widespread, having been added to several major programming languages and calculators.

Fundamentals

Definition

𝜏 is commonly defined as the ratio of a circle's circumference ${\textstyle {C}}$ to its radius ${\textstyle {r}}$:$$\tau ={\frac {C}{r}}$$A circle is defined as a closed curve formed by the set of all points in a plane that are a given distance from a fixed point, where the given distance is called the radius.

The distance around the circle is the circumference, and the ratio ${\textstyle {\frac {C}{r}}}$ is constant regardless of the circle's size. Thus, 𝜏 denotes the fixed relationship between the circumference of any circle and the fundamental defining property of that circle, the radius.

Units of angle

Some special angles in radians, stated in terms of 𝜏.

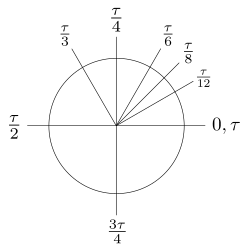
When radians are used as the unit of angular measure there are 𝜏 radians in one full turn of a circle, and the radian angle is aligned with the proportion of a full turn around the circle: ${\textstyle {\frac {\tau }{8}}}$ rad is an eighth of a turn; ${\textstyle {\frac {3\tau }{4}}}$ rad is three-quarters of a turn.

Relationship to π

As 𝜏 is exactly equal to 2π it shares many of the properties of π including being both an irrational and transcendental number.

History

The proposal to use the Greek letter 𝜏 as a circle constant representing 2π dates to Michael Hartl's 2010 publication, The Tau Manifesto, although the symbol had been independently suggested earlier by Joseph Lindenburg (c.1990), John Fisher (2004) and Peter Harremoës (2010).

Hartl offered two reasons for the choice of notation. First, τ is the number of radians in one turn, and both τ and turn begin with a /t/ sound. Second, τ visually resembles π, whose association with the circle constant is unavoidable.

Earlier proposals

There had been a number of earlier proposals for a new circle constant equal to 2π, together with varying suggestions for it's name and symbol.

In 2001, Robert Palais of the University of Utah proposed that π was "wrong" as the fundamental circle constant arguing instead that 2π was the proper value. His proposal used a "π with three legs" symbol to denote the constant ($\pi \!\;\!\!\!\pi =2\pi$), and referred to angles as fractions of a "turn" (${\tfrac {1}{4}}\pi \!\;\!\!\!\pi ={\tfrac {1}{4}}\,\mathrm {turn}$). Palais stated that the word "turn" served as both the name of the new constant and a reference to the ordinary language meaning of turn.

In 2008, Robert P. Crease proposed defining a constant as the ratio of circumference to radius, a idea supported by John Horton Conway. Crease used the Greek letter psi: $\psi =2\pi$.

The same year, Thomas Colignatus proposed the uppercase Greek letter theta, Θ, to represent 2π due to its visual resemblance of a circle. For a similar reason another proposal suggested the Phoenician and Hebrew letter teth, 𐤈 or ט, (from which the letter theta was derived), due to its connection with wheels and circles in ancient cultures.

Use of the symbol π to represent 6.28

See also: Pi § Adoption of the symbol π

The meaning of the symbol $\pi$ was not originally defined as the ratio of circumference to diameter, and at times was used in representations of the 6.28...constant.

Early works in circle geometry used the letter π to designate the perimeter (i.e., circumference) in different fractional representations of circle constants and in 1697 David Gregory used ⁠π/ρ⁠ (pi over rho) to denote the perimeter divided by the radius (6.28...).

Subsequently π came to be used as a single symbol to represent the ratios in whole. Leonhard Euler initially used the single letter π was to denote the constant 6.28... in his 1727 Essay Explaining the Properties of Air. Euler would later use the letter π for 3.14... in his 1736 Mechanica and 1748 Introductio in analysin infinitorum, though defined as half the circumference of a circle of radius 1 rather than the ratio of circumference to diameter. Elsewhere in Mechanica, Euler instead used the letter π for one-fourth of the circumference of a unit circle, or 1.57... . Usage of the letter π, sometimes for 3.14... and other times for 6.28..., became widespread, with the definition varying as late as 1761; afterward, π was standardized as being equal to 3.14... .

Notion using 𝜏

Proponents argue that while use of 𝜏 in place of 2π does not change any of the underlying mathematics, it does lead to simpler and more intuitive notation in many areas. Michael Hartl's Tau Manifesto gives many examples of formulas that are asserted to be clearer where τ is used instead of π.

Hartl and Robert Palais have argued that 𝜏 allows radian angles to be expressed more directly and in a way that makes clear the link between the radian measure and rotation around the unit circle. For instance, ⁠3τ/4⁠ rad can be easily interpreted as ⁠3/4⁠⁠ of a turn around the unit circle in contrast with the numerically equal ⁠⁠3π/2⁠⁠ rad, where the meaning could be obscured, particularly for children and students of mathematics.

Hartl has argued that the periodic trigonometric functions are simplified using 𝜏 as it aligns the function argument (radians) with the function period: sin θ repeats with period T = τ rad, reaches a maximum at ⁠T/4⁠=⁠τ/4⁠ rad and a minimum at ⁠3T/4⁠=⁠3τ/4⁠ rad.

Critics have argued that the formula for the area of a circle is more complicated when restated as A = ⁠1/2⁠𝜏r². Hartl and others respond that the ⁠1/2⁠ factor is meaningful, arising from either integration or geometric proofs for the area of a circle as half the circumference times the radius.

A common criticism of τ is that Euler's identity, e^iπ + 1 = 0, sometimes claimed to be "the most beautiful theorem in mathematics" is made less elegant rendered as e^iτ/2 + 1 = 0. Hartl has asserted that e^iτ = 1 (which he also called "Euler's identity") is more fundamental and meaningful. John Conway noted that Euler's identity is a specific case of the general formula of the n^th roots of unity, ⁿ√1 = e^iτk/n (k = 1,2,..,n), which he maintained is preferable and more economical than Euler’s.

Comparison of identities

The following table shows how various identities appear when τ = 2π is used instead of π. For a more complete list, see List of formulae involving π.

Formula	Using π	Using τ	Notes
Angle subtended by ⁠1/4⁠ of a circle	${\color {orangered}{\frac {\pi }{2}}}{\text{ rad}}$	${\color {orangered}{\frac {\tau }{4}}}{\text{ rad}}$	⁠τ/4⁠ rad = ⁠1/4⁠ turn
Circumference of a circle	$C={\color {orangered}2\pi }r$	$C={\color {orangered}\tau }r$	The length of an arc of angle θ is L = θr.
Area of a circle	$A={\color {orangered}\pi }r^{2}$	$A={\color {orangered}{\frac {1}{2}}\tau }r^{2}$	The area of a sector of angle θ is A = ⁠1/2⁠θr2.
Area of a regular n-gon with unit circumradius	$A={\frac {n}{2}}\sin {\frac {\color {orangered}2\pi }{n}}$	$A={\frac {n}{2}}\sin {\frac {\color {orangered}\tau }{n}}$
n-ball and n-sphere volume recurrence relation	$V_{n}(r)={\frac {r}{n}}S_{n-1}(r)$ $S_{n}(r)={\color {orangered}2\pi }rV_{n-1}(r)$	$V_{n}(r)={\frac {r}{n}}S_{n-1}(r)$ $S_{n}(r)={\color {orangered}\tau }rV_{n-1}(r)$	V0(r) = 1 S0(r) = 2
Cauchy's integral formula	$f(a)={\frac {1}{{\color {orangered}2\pi }i}}\oint _{\gamma }{\frac {f(z)}{z-a}}\,dz$	$f(a)={\frac {1}{{\color {orangered}\tau }i}}\oint _{\gamma }{\frac {f(z)}{z-a}}\,dz$	$\gamma$ is the boundary of a disk containing $a$ in the complex plane.
Standard normal distribution	$\varphi (x)={\frac {1}{\sqrt {\color {orangered}2\pi }}}e^{-{\frac {x^{2}}{2}}}$	$\varphi (x)={\frac {1}{\sqrt {\color {orangered}\tau }}}e^{-{\frac {x^{2}}{2}}}$
Stirling's approximation	$n!\sim {\sqrt {{\color {orangered}2\pi }n}}\left({\frac {n}{e}}\right)^{n}$	$n!\sim {\sqrt {{\color {orangered}\tau }n}}\left({\frac {n}{e}}\right)^{n}$
nth roots of unity	$e^{{\color {orangered}2\pi }i{\frac {k}{n}}}=\cos {\frac {{\color {orangered}2}k{\color {orangered}\pi }}{n}}+i\sin {\frac {{\color {orangered}2}k{\color {orangered}\pi }}{n}}$	$e^{{\color {orangered}\tau }i{\frac {k}{n}}}=\cos {\frac {k{\color {orangered}\tau }}{n}}+i\sin {\frac {k{\color {orangered}\tau }}{n}}$
Planck constant	$h={\color {orangered}2\pi }\hbar$	$h={\color {orangered}\tau }\hbar$	ħ is the reduced Planck constant.
Angular frequency	$\omega ={\color {orangered}2\pi }f$	$\omega ={\color {orangered}\tau }f$
Riemann's functional equation	$$\zeta (s)={\color {orangered}2^{s}\pi ^{s-1}}\ \sin \left(s{\color {orangered}{\frac {\pi }{2}}}\right)\ \Gamma (1-s)\ \zeta (1-s)$$	$$\zeta (s)={\color {orangered}2\tau ^{s-1}}\ \sin \left(s{\color {orangered}{\frac {\tau }{4}}}\right)\ \Gamma (1-s)\ \zeta (1-s)$$	$2^{s}({\frac {\tau }{2}})^{s-1}$ reduces to $2\tau ^{s-1}$

In culture

𝜏 has made numerous appearances in culture. It is celebrated annually on June 28, known as Tau Day. Supporters of 𝜏 are called tauists. 𝜏 has been covered in videos by Vi Hart, Numberphile, SciShow, Steve Mould, Khan Academy, and 3Blue1Brown, and it has appeared in the comics xkcd, Saturday Morning Breakfast Cereal, and Sally Forth. The Massachusetts Institute of Technology usually announces admissions on March 14 at 6:28 p.m., which is on Pi Day at Tau Time. Peter Harremoës has used τ in a mathematical research article which was granted Editor's award of the year.

In programming languages and calculators

The following table documents various programming languages that have implemented the circle constant for converting between turns and radians. All of the languages below support the name "Tau" in some casing, but Processing also supports "TWO_PI" and Raku also supports the symbol "τ" for accessing the same value.

Language	Identifiers	First Version	Year Released
C# / .NET	System.Math.Tau and System.MathF.Tau	5.0	2020
Crystal	TAU	0.36.0	2021
Eiffel	math_constants.Tau	Curtiss	Not yet released
GDScript	TAU	Godot 3.0	2018
Java	Math.TAU	19	2022
Nim	TAU	0.14.0	2016
Processing	TAU and TWO_PI	2.0	2013
Python	math.tau	3.6	2016
Raku	tau and τ
Rust	std::f64::consts::TAU	1.47.0	2020
Zig	std.math.tau	0.6.0	2019

The constant τ is made available in the Google calculator, Desmos graphing calculator, and the iPhone's Convert Angle option expresses the turn as τ.

External links

• The Tau Manifesto